Vidéos sur divers thèmes de mathématique du collège
Des vidéos de cours et d'exercices de 4e sur les probabilités et l'analyse combinatoire.
Un cour sur les probabilités conditionnelles du programme Français.
Table des matières Liens internes à cette page
- Introduction
°) Thème : lim (x->0) sin(x) / x = 1, démonstration, version longue
°) Thème : lim (x->0) sin(x) / x = 1, démonstration, version courte
°) Théorème : "dérivable implique continue", démonstration
°) Théorème : (f*g)' = f'*g + f*g', démonstration
°) Théorème des accroissement finis, énoncé et démonstration
°) Démonstration que f(x)=x^n => f'(x)=n*x^(n-1), pour n entier
°) Démonstration que deux primitives diffèrent d'une constante
°) Thème : l'aire sous une courbe, sommes minorantes, sommes Majorantes, intégrale définie
°) Démonstration du théorème fondamental du calcul intégral
°) Démonstration du théorème de la moyenne
°) Transformations linéaires de R2
°) Composée d'applications linéaires de R2 et réciproque
°) Matrice d'une symétrie orthogonale
°) Analyse combinatoire
°) Axiomes fondateurs et théorèmes du calcul des probabilités
°) Théorème de Bayes sur la probabilité des causes
°) Variable aléatoire discrète
°) Loi binomiale
°) Pourquoi -1 * -1 = +1 ?
Pour la curiosité ...
°) Démonstration de règles de dérivation selon la formulation de Carathéodory. (f*g)'= f'*g+f*g'.
Cette approche est beaucoup plus simple que l'approche usuelle, mais plus abstraite.
°) Formulation de Carathéodory pour démontrer (f/g)' = (f'*g - f*g')/g^2.
°) Formulation de Carathéodory pour démontrer (g ° f)' = (g' ° f)*f' et (f^n)' = n*f^(n-1) * f'.
°) Formulation de Carathéodory pour démontrer (rf)' = (1 / f) ° (rf) et dérivable=>continue.
°) 4 curiosités mathématiques
°)
°) Introduction Top
Les buts de cette page est de fournir quelques vidéos sur divers thèmes de mathématiques.
En particulier, certaines démonstrations des thèmes de 3ème et 4ème années sont faites dans ces vidéos.
Thème : lim (x->0) sin(x) / x = 1, démonstration, version longue Top
Traitement du thème : lim (x->0) sin(x) / x = 1, avec une démonstration. Version longue, de 16'25''.
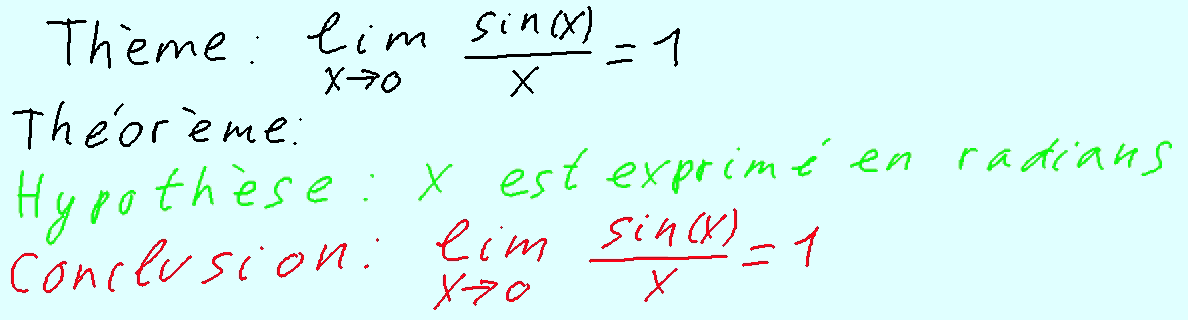
Thème : lim (x->0) sin(x) / x = 1, démonstration, version courte Top
Traitement du thème : lim (x->0) sin(x) / x = 1, avec une démonstration. Version courte, de 9'.
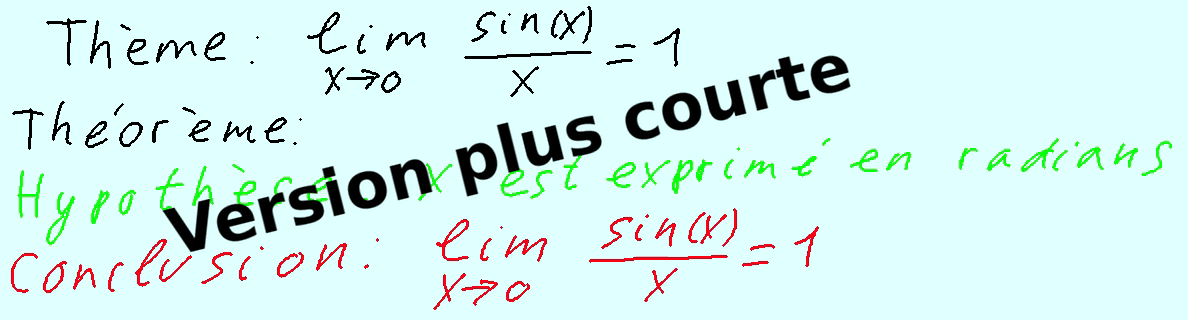
Théorème : "dérivable implique continue", démonstration Top
Énoncé et démonstration du théorème disant qu'une fonction dérivable en un point
est aussi continue en ce point.
Montre que la réciproque est fausse. Durée : 16'51''.

Théorème : (f*g)' = f'*g + f*g', démonstration Top
Énoncé et démonstration du théorème : (f*g)' = f'*g + f*g'.
Utilisation pour calculer la dérivée de h(x) = x*x et de j(x) = x*x*x, de 16'20''.
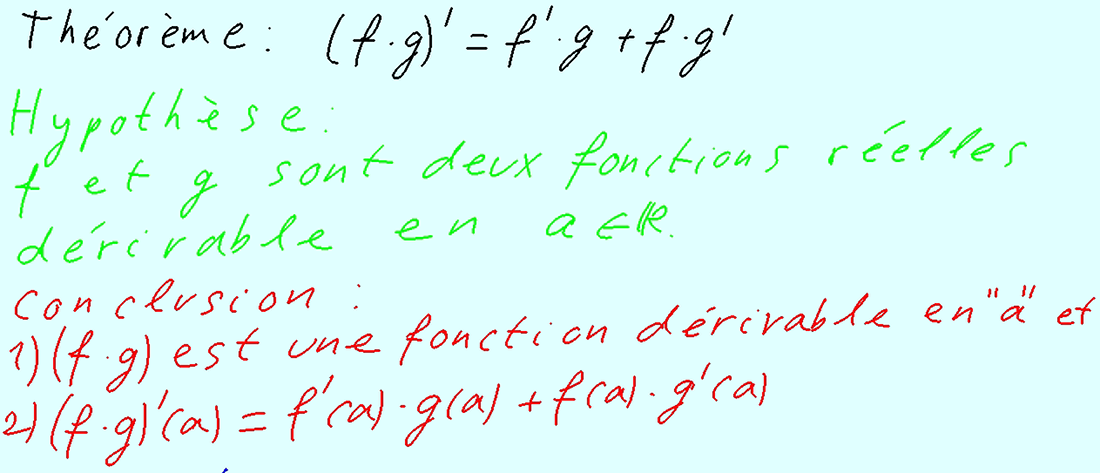
Théorème des accroissement finis, énoncé et démonstration Top
Énoncé et démonstration du théorème des accroissement finis,
dit également "théorème de Lagrange", de 13'35''.

Démonstration que f(x)=x^n => f'(x)=n*x^(n-1), pour n entier Top
Démonstration de la formule de dérivation de la fonction "mise à la puissance n", pour n entier.
Deux démonstrations sont données pour n entier positif.
Une démonstration est donnée pour n entier négatif.
Pour le cas où n est rationnel,
on peut utiliser la règle de dérivation de fonctions réciproque et
la règle de dérivation de la composition de fonctions.
Cette partie n'est pas faite dans la vidéo.
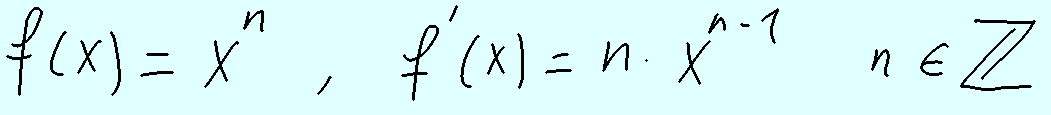
Démonstration que deux primitives diffèrent d'une constante Top
Démonstration du faite que deux primitives d'une même fonctions sont égales à une constante près.

Thème : l'aire sous une courbe, sommes minorantes, sommes Majorantes, intégrale définie Top
Définition des notions de sommes minorantes et de sommes Majorantes,
correspondant à des aires minorantes et des aires Majorantes.
Définition précise de ce qu'est l'aire entre les verticales x = a ; x = b ; l'axe des abscisses
et la courbe d'une fonction. L'aire étant une aire algébrique.
Définition de la notion d'intégrale définie de a à b.
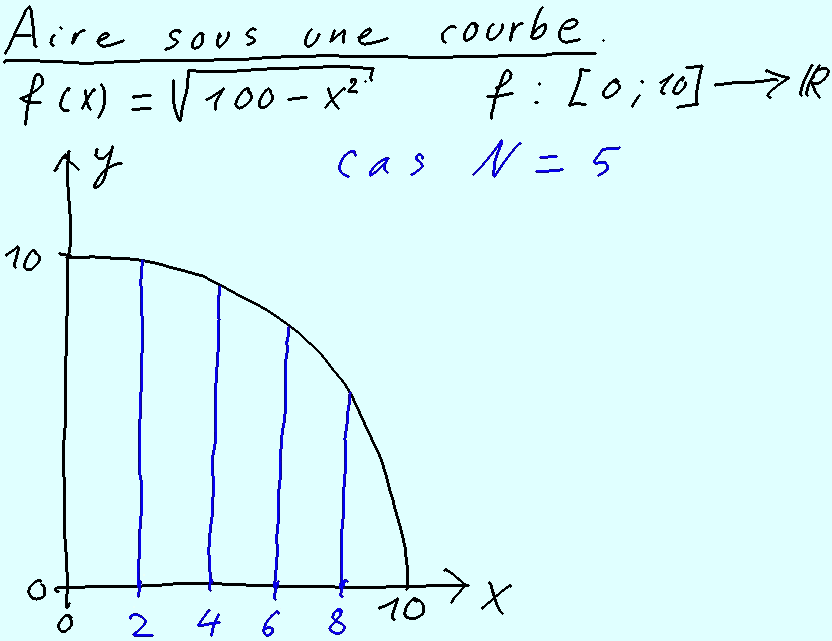
Démonstration du théorème fondamental du calcul intégral Top
Énoncé et démonstration du théorème fondamental du calcul intégral.
Ce théorème indique comment calculer facilement une intégrale définie sur [a ; b],
si on connait une primitive de la fonction à intégrer.

Démonstration du théorème de la moyenne Top
Énoncé et démonstration du théorème de la moyenne qui donne un lien entre l'aire sous une courbe
et l'aire d'une rectangle.

Définition d'une transformation linéaire de R2 et lien avec les matrices.

Composée d'applications linéaires de R2 et réciproque Top
Liens entre les matrices et les composée d'applications linéaires de R2.
Erratum : à 20 minutes 8 secondes, j'écris "+0,4 * 0,8". Correct est : "+0,4 * 0,6". Le reste est correct.

Matrice d'une symétrie orthogonale Top
Détermination de la matrice d'une symétrie orthogonale d'axe y = a x de R2.
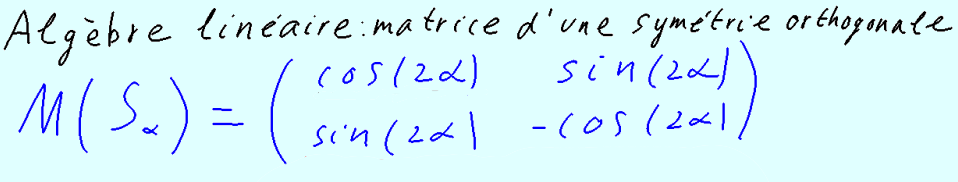
Analyse combinatoire Top
Éléments d'analyse combinatoire.

Axiomes fondateurs et théorèmes du calcul des probabilités Top
Énoncé des trois axiomes de la théorie des probabilités et démonstrations de trois théorèmes qui en découlent.
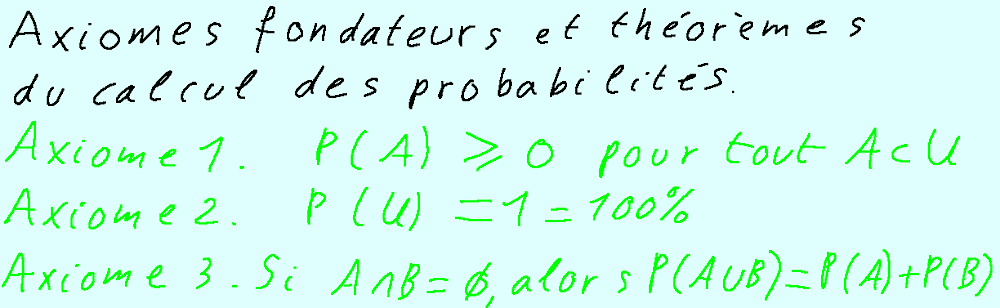
Théorème de Bayes sur la probabilité des causes Top
Présentation et démonstration du théorème de Bayes.

Variable aléatoire discrète Top
Présentation de la notion de variable aléatoire discrète et définitions.

Loi binomiale Top
Présentation de la loi binomiale. Exemple, espérance et variance.

Pourquoi -1 * -1 = +1 ? Top
Justifie pourquoi le produit -1 * -1 = +1.
Donne trois justifications.
Continue avec un pas dans le monde des nombres imaginaires ( i ).
Voici une vidéo en anglais qui traite du même sujet, faite par Mathloger :
A negative times a negative is a ... ?
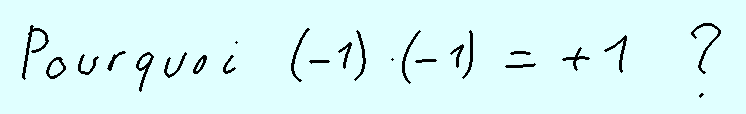
Démonstration de règles de dérivation selon la formulation de Carathéodory. (f*g)'= f'*g+f*g' Top
En utilisant la formulation de Carathéodory de 1950,
la démonstration des règles de dérivation est beaucoup plus simple,
mais un peu plus abstraite.
Cette vidéo explique cette formulation de Carathéodory,
puis démontre les règles de dérivations :
(f+g)'(a) = f'(a) + g'(a) et
(f*g)'(a) = f'(a) * g(a) + f(a) * g'(a)

Formulation de Carathéodory pour démontrer (f/g)' = (f'*g - f*g')/g^2 Top
En utilisant la formulation de Carathéodory de 1950,
la démonstration des règles de dérivation est beaucoup plus simple,
mais un peu plus abstraite.
Cette vidéo démontre les règles de dérivations :
(1/g)'(a) = -g'(a) / g^2(a) et
(f/g)'(a) = (f'(a) * g(a) - f(a) * g'(a)) / g^2(a)

Formulation de Carathéodory pour démontrer (g ° f)' = (g' ° f)*f' et (f^n)' = n*f^(n-1) * f' Top
En utilisant la formulation de Carathéodory de 1950,
la démonstration des règles de dérivation est beaucoup plus simple,
mais un peu plus abstraite.
Cette vidéo démontre les règles de dérivations :
(g°f)'(a) = g'(f(a)) * f'(a) et
(f^n)'(a) = n * f^(n-1)(a) * f'(a)

Formulation de Carathéodory pour démontrer (rf)' = (1 / f') ° (rf) et dérivable=>continue Top
En utilisant la formulation de Carathéodory de 1950,
la démonstration des règles de dérivation est beaucoup plus simple,
mais un peu plus abstraite.
Cette vidéo démontre la règle de dérivation :
(rf)'(f(a)) = 1/f'(a) et
f dérivable en a => f continue en a.

4 curiosités mathématiques Top
Justification que la dérivée de la fonction racine carré égale 1 sur 2 fois la racine carrée.
Justification que la dérivée de la fonction sinus égale la fonction cosinus.
Justification que la dérivée de la fonction cosinus égale la fonction moins sinus.
Justification que la dérivée de la fonction exponnentielle (exp(x) = e^x) est égale à elle-même.
Justification que la dérivée de la fonction logarithme naturel (ln(x) égale à la fonction inverse ( ln'(x) = 1/x).
Aucune des justification précédente n'est rigoureuse, il manque des étapes.
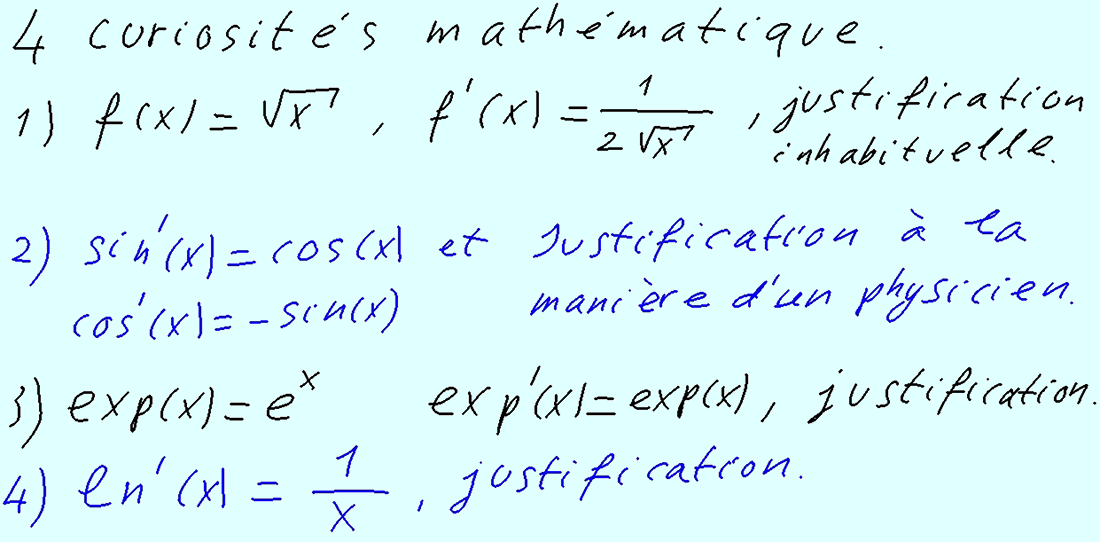
Plan du Site :
Home
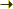 coursmath_ref
coursmath_ref
 videos_math.html
( = https://www.juggling.ch/gisin/coursmath_ref/videos_math.html )
videos_math.html
( = https://www.juggling.ch/gisin/coursmath_ref/videos_math.html )
Page mise à jour le 28 mai 2022 par Bernard Gisin
( Envoyer un e-mail )
Hébergement par : www.infomaniak.ch
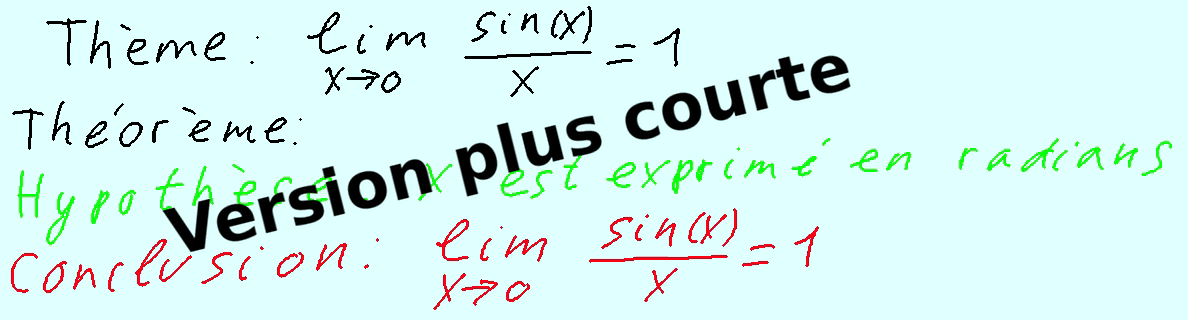

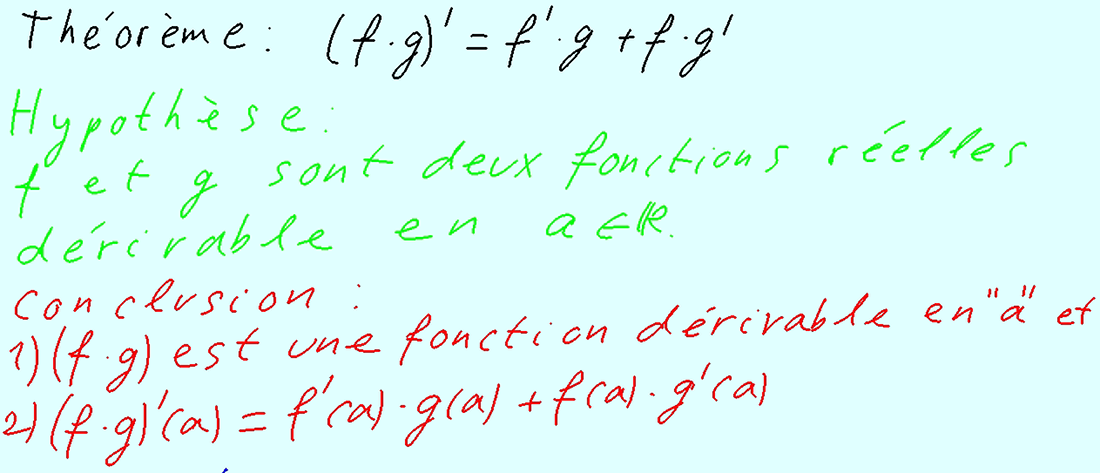

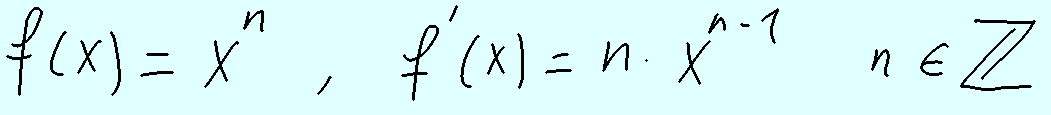

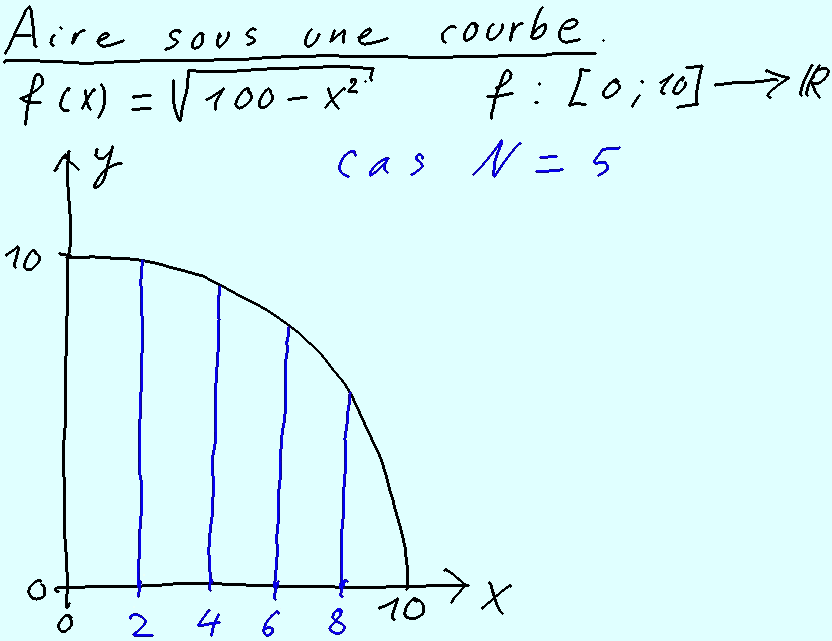




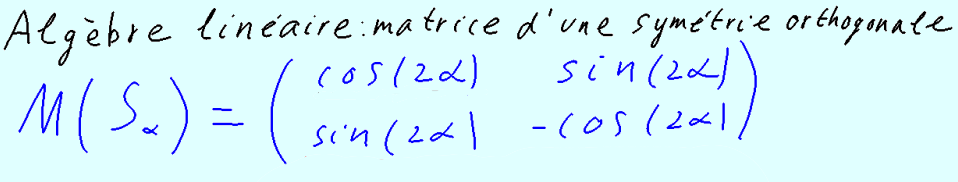

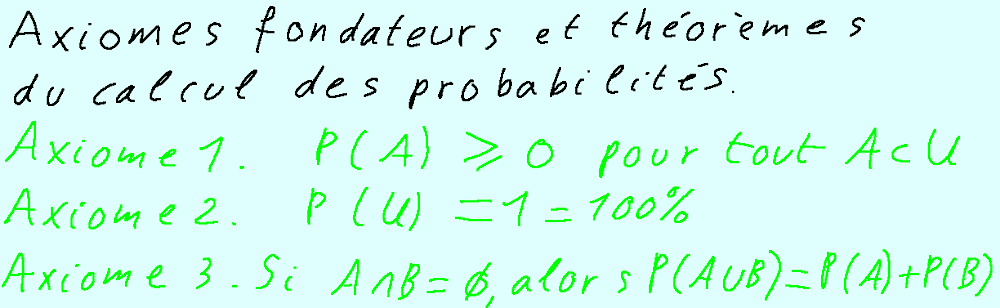



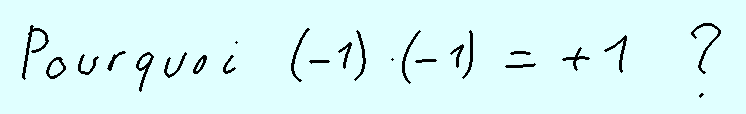




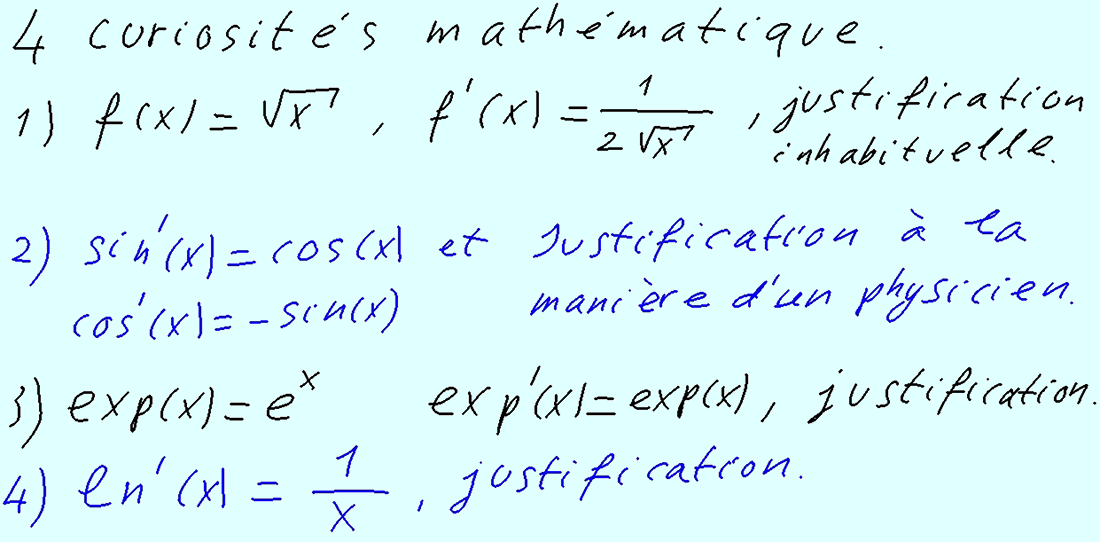
![]() coursmath_ref
coursmath_ref
![]() videos_math.html
( = https://www.juggling.ch/gisin/coursmath_ref/videos_math.html )
videos_math.html
( = https://www.juggling.ch/gisin/coursmath_ref/videos_math.html )