ON THE ELECTRODYNAMICS
OF MOVING BODIES
By A. Einstein
June 30, 1905
Examples of this sort, together with the unsuccessful attempts to discover any motion of the earth relatively to the ``light medium,'' suggest that the phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest. They suggest rather that, as has already been shown to the first order of small quantities, the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good.1 We will raise this conjecture (the purport of which will hereafter be called the ``Principle of Relativity'') to the status of a postulate, and also introduce another postulate, which is only apparently irreconcilable with the former, namely, that light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body. These two postulates suffice for the attainment of a simple and consistent theory of the electrodynamics of moving bodies based on Maxwell's theory for stationary bodies. The introduction of a ``luminiferous ether'' will prove to be superfluous inasmuch as the view here to be developed will not require an ``absolutely stationary space'' provided with special properties, nor assign a velocity-vector to a point of the empty space in which electromagnetic processes take place.
The theory to be developed is based--like all electrodynamics--on the kinematics of the rigid body, since the assertions of any such theory have to do with the relationships between rigid bodies (systems of co-ordinates), clocks, and electromagnetic processes. Insufficient consideration of this circumstance lies at the root of the difficulties which the electrodynamics of moving bodies at present encounters.
I. KINEMATICAL PART
§ 1. Definition of Simultaneity
If a material point is at rest relatively to this system of co-ordinates, its position can be defined relatively thereto by the employment of rigid standards of measurement and the methods of Euclidean geometry, and can be expressed in Cartesian co-ordinates.
If we wish to describe the motion of a material point, we give the values of its co-ordinates as functions of the time. Now we must bear carefully in mind that a mathematical description of this kind has no physical meaning unless we are quite clear as to what we understand by ``time.'' We have to take into account that all our judgments in which time plays a part are always judgments of simultaneous events. If, for instance, I say, ``That train arrives here at 7 o'clock,'' I mean something like this: ``The pointing of the small hand of my watch to 7 and the arrival of the train are simultaneous events.''3
It might appear possible to overcome all the difficulties attending the definition of ``time'' by substituting ``the position of the small hand of my watch'' for ``time.'' And in fact such a definition is satisfactory when we are concerned with defining a time exclusively for the place where the watch is located; but it is no longer satisfactory when we have to connect in time series of events occurring at different places, or--what comes to the same thing--to evaluate the times of events occurring at places remote from the watch.
We might, of course, content ourselves with time values determined by an observer stationed together with the watch at the origin of the co-ordinates, and co-ordinating the corresponding positions of the hands with light signals, given out by every event to be timed, and reaching him through empty space. But this co-ordination has the disadvantage that it is not independent of the standpoint of the observer with the watch or clock, as we know from experience. We arrive at a much more practical determination along the following line of thought.
If at the point A of space there is a clock, an observer at A can determine
the time values of events in the immediate proximity of A by finding the
positions of the hands which are simultaneous with these events. If there
is at the point B of space another clock in all respects resembling the
one at A, it is possible for an observer at B to determine the time values
of events in the immediate neighbourhood of B. But it is not possible without
further assumption to compare, in respect of time, an event at A with an
event at B. We have so far defined only an ``A time'' and a ``B time.''
We have not defined a common ``time'' for A and B, for the latter cannot
be defined at all unless we establish by definition that the ``time''
required by light to travel from A to B equals the ``time'' it requires
to travel from B to A. Let a ray of light start at the ``A time'' ![]() from
A towards B, let it at the ``B time''
from
A towards B, let it at the ``B time'' ![]() be reflected at B in the direction of A, and arrive again at A at the ``A
time''
be reflected at B in the direction of A, and arrive again at A at the ``A
time'' ![]() .
.
In accordance with definition the two clocks synchronize if
- If the clock at B synchronizes with the clock at A, the clock at A synchronizes with the clock at B.
- If the clock at A synchronizes with the clock at B and also with the clock at C, the clocks at B and C also synchronize with each other.
In agreement with experience we further assume the quantity
It is essential to have time defined by means of stationary clocks in the stationary system, and the time now defined being appropriate to the stationary system we call it ``the time of the stationary system.''
§ 2. On the Relativity of Lengths and Times
- The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems of co-ordinates in uniform translatory motion.
- Any ray of light moves in the ``stationary'' system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body. Hence
- (a)
- The observer moves together with the given measuring-rod and the rod to be measured, and measures the length of the rod directly by superposing the measuring-rod, in just the same way as if all three were at rest.
- (b)
- By means of stationary clocks set up in the stationary system and synchronizing in accordance with § 1, the observer ascertains at what points of the stationary system the two ends of the rod to be measured are located at a definite time. The distance between these two points, measured by the measuring-rod already employed, which in this case is at rest, is also a length which may be designated ``the length of the rod.''
The length to be discovered by the operation (b) we will call ``the length of the (moving) rod in the stationary system.'' This we shall determine on the basis of our two principles, and we shall find that it differs from l.
Current kinematics tacitly assumes that the lengths determined by these two operations are precisely equal, or in other words, that a moving rigid body at the epoch t may in geometrical respects be perfectly represented by the same body at rest in a definite position.
We imagine further that at the two ends A and B of the rod, clocks are placed which synchronize with the clocks of the stationary system, that is to say that their indications correspond at any instant to the ``time of the stationary system'' at the places where they happen to be. These clocks are therefore ``synchronous in the stationary system.''
We imagine further that with each clock there is a moving observer,
and that these observers apply to both clocks the criterion established
in
§ 1 for the synchronization of two clocks.
Let a ray of light depart from A at the time4![]() ,
let it be reflected at B at the time
,
let it be reflected at B at the time ![]() ,
and reach A again at the time
,
and reach A again at the time ![]() .
Taking into consideration the principle of the constancy of the velocity
of light we find that
.
Taking into consideration the principle of the constancy of the velocity
of light we find that
So we see that we cannot attach any absolute signification to the concept of simultaneity, but that two events which, viewed from a system of co-ordinates, are simultaneous, can no longer be looked upon as simultaneous events when envisaged from a system which is in motion relatively to that system.
§ 3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former
Now to the origin of one of the two systems (k) let a constant velocity v be imparted in the direction of the increasing x of the other stationary system (K), and let this velocity be communicated to the axes of the co-ordinates, the relevant measuring-rod, and the clocks. To any time of the stationary system K there then will correspond a definite position of the axes of the moving system, and from reasons of symmetry we are entitled to assume that the motion of k may be such that the axes of the moving system are at the time t (this ``t'' always denotes a time of the stationary system) parallel to the axes of the stationary system.
We now imagine space to be measured from the stationary system K by
means of the stationary measuring-rod, and also from the moving system
k
by means of the measuring-rod moving with it; and that we thus obtain the
co-ordinates x, y, z, and![]() ,
,![]() ,
,![]() respectively. Further, let the time t of the stationary system be
determined for all points thereof at which there are clocks by means of
light signals in the manner indicated in
§ 1;
similarly let the time
respectively. Further, let the time t of the stationary system be
determined for all points thereof at which there are clocks by means of
light signals in the manner indicated in
§ 1;
similarly let the time ![]() of the moving system be determined for all points of the moving system
at which there are clocks at rest relatively to that system by applying
the method, given in
§ 1, of light signals
between the points at which the latter clocks are located.
of the moving system be determined for all points of the moving system
at which there are clocks at rest relatively to that system by applying
the method, given in
§ 1, of light signals
between the points at which the latter clocks are located.
To any system of values x, y, z, t, which
completely defines the place and time of an event in the stationary system,
there belongs a system of values![]() ,
,![]() ,
,![]()
![]() ,
determining that event relatively to the system k, and our task
is now to find the system of equations connecting these quantities.
,
determining that event relatively to the system k, and our task
is now to find the system of equations connecting these quantities.
In the first place it is clear that the equations must be linear on account of the properties of homogeneity which we attribute to space and time.
If we place x'=x-vt, it is clear that a point at
rest in the system k must have a system of values x', y,
z, independent of time. We first define ![]() as a function of x', y, z, and t. To do this
we have to express in equations that
as a function of x', y, z, and t. To do this
we have to express in equations that ![]() is nothing else than the summary of the data of clocks at rest in system
k, which have been synchronized according to the rule given in
§
1.
is nothing else than the summary of the data of clocks at rest in system
k, which have been synchronized according to the rule given in
§
1.
From the origin of system k let a ray be emitted at the time ![]() along the X-axis to x', and at the time
along the X-axis to x', and at the time ![]() be reflected thence to the origin of the co-ordinates, arriving there at
the time
be reflected thence to the origin of the co-ordinates, arriving there at
the time ![]() ;
we then must have
;
we then must have ![]() ,
or, by inserting the arguments of the function
,
or, by inserting the arguments of the function ![]() and applying the principle of the constancy of the velocity of light in
the stationary system:--
and applying the principle of the constancy of the velocity of light in
the stationary system:--
An analogous consideration--applied to the axes of Y and Z--it being
borne in mind that light is always propagated along these axes, when viewed
from the stationary system, with the velocity ![]() gives
us
gives
us
With the help of this result we easily determine the quantities![]() ,
,![]() ,
,![]() by expressing in equations that light (as required by the principle of
the constancy of the velocity of light, in combination with the principle
of relativity) is also propagated with velocity c when measured
in the moving system. For a ray of light emitted at the time
by expressing in equations that light (as required by the principle of
the constancy of the velocity of light, in combination with the principle
of relativity) is also propagated with velocity c when measured
in the moving system. For a ray of light emitted at the time![]() in the direction of the increasing
in the direction of the increasing ![]()
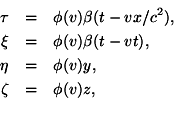
We now have to prove that any ray of light, measured in the moving system, is propagated with the velocity c, if, as we have assumed, this is the case in the stationary system; for we have not as yet furnished the proof that the principle of the constancy of the velocity of light is compatible with the principle of relativity.
At the time ![]() ,
when the origin of the co-ordinates is common to the two systems, let a
spherical wave be emitted therefrom, and be propagated with the velocity
c in system K. If (x, y, z) be a point just
attained by this wave, then
,
when the origin of the co-ordinates is common to the two systems, let a
spherical wave be emitted therefrom, and be propagated with the velocity
c in system K. If (x, y, z) be a point just
attained by this wave, then
In the equations of transformation which have been developed there enters
an unknown function ![]() of v, which we will now determine.
of v, which we will now determine.
For this purpose we introduce a third system of co-ordinates![]() ,
which relatively to the system k is in a state of parallel translatory
motion parallel to the axis of X, such that the origin of co-ordinates
of system k moves with velocity -v on the axis of X. At the
time t=0 let all three origins coincide, and when t=x=y=z=0
let the time t' of the system
,
which relatively to the system k is in a state of parallel translatory
motion parallel to the axis of X, such that the origin of co-ordinates
of system k moves with velocity -v on the axis of X. At the
time t=0 let all three origins coincide, and when t=x=y=z=0
let the time t' of the system ![]() be zero. We call the co-ordinates, measured in the system
be zero. We call the co-ordinates, measured in the system ![]() ,
x',
y', z', and by a twofold application of our equations of
transformation we obtain
,
x',
y', z', and by a twofold application of our equations of
transformation we obtain
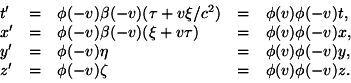
and
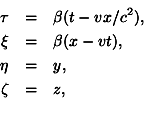
§ 4. Physical Meaning of the Equations Obtained in Respect to Moving Rigid Bodies and Moving Clocks
It is clear that the same results hold good of bodies at rest in the ``stationary'' system, viewed from a system in uniform motion.
Further, we imagine one of the clocks which are qualified to mark the
time t when at rest relatively to the stationary system, and the
time ![]() when at rest relatively to the moving system, to be located at the origin
of the co-ordinates of k, and so adjusted that it marks the time
when at rest relatively to the moving system, to be located at the origin
of the co-ordinates of k, and so adjusted that it marks the time ![]() .
What is the rate of this clock, when viewed from the stationary system?
.
What is the rate of this clock, when viewed from the stationary system?
Between the quantities x, t, and ![]() ,
which refer to the position of the clock, we have, evidently, x=vt
and
,
which refer to the position of the clock, we have, evidently, x=vt
and
From this there ensues the following peculiar consequence. If at the
points A and B of K there are stationary clocks which, viewed in the stationary
system, are synchronous; and if the clock at A is moved with the velocity
v along the line AB to B, then on its arrival at B the two clocks
no longer synchronize, but the clock moved from A to B lags behind the
other which has remained at B by ![]() (up
to magnitudes of fourth and higher order), t being the time occupied
in the journey from A to B.
(up
to magnitudes of fourth and higher order), t being the time occupied
in the journey from A to B.
It is at once apparent that this result still holds good if the clock moves from A to B in any polygonal line, and also when the points A and B coincide.
If we assume that the result proved for a polygonal line is also valid
for a continuously curved line, we arrive at this result: If one of two
synchronous clocks at A is moved in a closed curve with constant velocity
until it returns to A, the journey lasting t seconds, then by the
clock which has remained at rest the travelled clock on its arrival at
A will be ![]() second slow. Thence we conclude that a balance-clock7
at the equator must go more slowly, by a very small amount, than a precisely
similar clock situated at one of the poles under otherwise identical conditions.
second slow. Thence we conclude that a balance-clock7
at the equator must go more slowly, by a very small amount, than a precisely
similar clock situated at one of the poles under otherwise identical conditions.
§ 5. The Composition of Velocities
Required: the motion of the point relatively to the system K. If with the help of the equations of transformation developed in § 3 we introduce the quantities x, y, z, t into the equations of motion of the point, we obtain
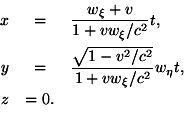
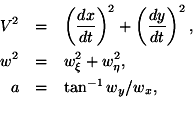
We have now deduced the requisite laws of the theory of kinematics corresponding to our two principles, and we proceed to show their application to electrodynamics.
II. ELECTRODYNAMICAL PART
§ 6. Transformation of the Maxwell-Hertz Equations for Empty Space. On the Nature of the Electromotive Forces Occurring in a Magnetic Field During Motion

If we apply to these equations the transformation developed in § 3, by referring the electromagnetic processes to the system of co-ordinates there introduced, moving with the velocity v, we obtain the equations
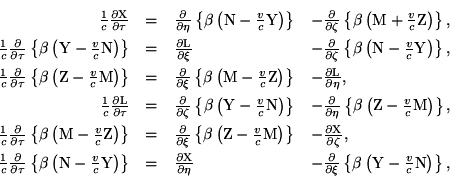

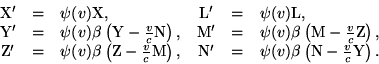
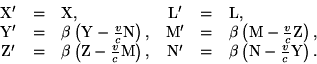
- If a unit electric point charge is in motion in an electromagnetic field, there acts upon it, in addition to the electric force, an ``electromotive force'' which, if we neglect the terms multiplied by the second and higher powers of v/c, is equal to the vector-product of the velocity of the charge and the magnetic force, divided by the velocity of light. (Old manner of expression.)
- If a unit electric point charge is in motion in an electromagnetic field, the force acting upon it is equal to the electric force which is present at the locality of the charge, and which we ascertain by transformation of the field to a system of co-ordinates at rest relatively to the electrical charge. (New manner of expression.)
The analogy holds with ``magnetomotive forces.'' We see that electromotive
force plays in the developed theory merely the part of an auxiliary concept,
which owes its introduction to the circumstance that electric and magnetic
forces do not exist independently of the state of motion of the system
of co-ordinates.
Furthermore it is clear that the asymmetry mentioned in the introduction as arising when we consider the currents produced by the relative motion of a magnet and a conductor, now disappears. Moreover, questions as to the ``seat'' of electrodynamic electromotive forces (unipolar machines) now have no point.
§ 7. Theory of Doppler's Principle and of Aberration
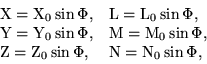
Applying the equations of transformation found in § 6 for electric and magnetic forces, and those found in § 3 for the co-ordinates and the time, we obtain directly
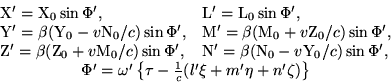

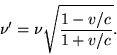
If we call the angle between the wave-normal (direction of the ray)
in the moving system and the connecting line ``source-observer'' ![]() ,
the equation for l' assumes the form
,
the equation for l' assumes the form
§ 8. Transformation of the Energy of Light Rays. Theory of the Pressure of Radiation Exerted on Perfect Reflectors
The spherical surface--viewed in the moving system--is an ellipsoidal
surface, the equation for which, at the time![]() ,
is
,
is
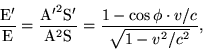
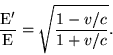
Now let the co-ordinate plane ![]() be a perfectly reflecting surface, at which the plane waves considered
in
§ 7 are reflected. We seek for the pressure
of light exerted on the reflecting surface, and for the direction, frequency,
and intensity of the light after reflexion.
be a perfectly reflecting surface, at which the plane waves considered
in
§ 7 are reflected. We seek for the pressure
of light exerted on the reflecting surface, and for the direction, frequency,
and intensity of the light after reflexion.
Let the incidental light be defined by the quantities A, ![]() ,
,![]() (referred to system K). Viewed from k the corresponding quantities
are
(referred to system K). Viewed from k the corresponding quantities
are
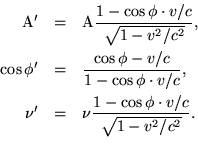
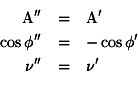
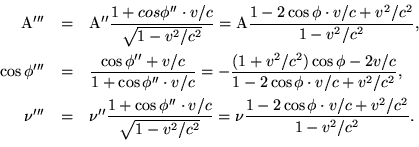
§ 9. Transformation of the Maxwell-Hertz Equations when Convection-Currents are Taken into Account

Let these equations be valid in the system K, and transform them, with the assistance of the equations of transformation given in §§ 3 and 6, to the system k. We then obtain the equations

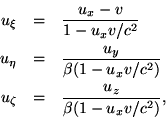
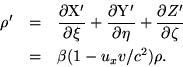
In addition I may briefly remark that the following important law may easily be deduced from the developed equations: If an electrically charged body is in motion anywhere in space without altering its charge when regarded from a system of co-ordinates moving with the body, its charge also remains--when regarded from the ``stationary'' system K--constant.
§ 10. Dynamics of the Slowly Accelerated Electron
If the electron is at rest at a given epoch, the motion of the electron ensues in the next instant of time according to the equations
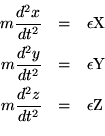
Now, secondly, let the velocity of the electron at a given epoch be v. We seek the law of motion of the electron in the immediately ensuing instants of time.
Without affecting the general character of our considerations, we may and will assume that the electron, at the moment when we give it our attention, is at the origin of the co-ordinates, and moves with the velocity v along the axis of X of the system K. It is then clear that at the given moment (t=0) the electron is at rest relatively to a system of co-ordinates which is in parallel motion with velocity v along the axis of X.
From the above assumption, in combination with the principle of relativity, it is clear that in the immediately ensuing time (for small values of t) the electron, viewed from the system k, moves in accordance with the equations
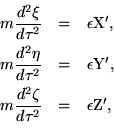
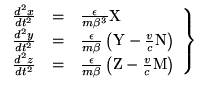 |
Taking the ordinary point of view we now inquire as to the ``longitudinal'' and the ``transverse'' mass of the moving electron. We write the equations (A) in the form
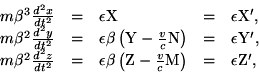
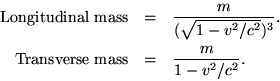
We remark that these results as to the mass are also valid for ponderable material points, because a ponderable material point can be made into an electron (in our sense of the word) by the addition of an electric charge, no matter how small.
We will now determine the kinetic energy of the electron. If an electron
moves from rest at the origin of co-ordinates of the system K along the
axis of X under the action of an electrostatic force X, it is clear that
the energy withdrawn from the electrostatic field has the value ![]() .
As the electron is to be slowly accelerated, and consequently may not give
off any energy in the form of radiation, the energy withdrawn from the
electrostatic field must be put down as equal to the energy of motion W
of the electron. Bearing in mind that during the whole process of motion
which we are considering, the first of the equations (A) applies,
we therefore obtain
.
As the electron is to be slowly accelerated, and consequently may not give
off any energy in the form of radiation, the energy withdrawn from the
electrostatic field must be put down as equal to the energy of motion W
of the electron. Bearing in mind that during the whole process of motion
which we are considering, the first of the equations (A) applies,
we therefore obtain
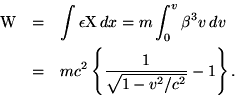
This expression for the kinetic energy must also, by virtue of the argument stated above, apply to ponderable masses as well.
We will now enumerate the properties of the motion of the electron which result from the system of equations (A), and are accessible to experiment.
-
From the second equation of the system (A) it follows that an electric
force Y and a magnetic force N have an equally strong deflective action
on an electron moving with the velocity v, when
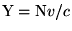 .
Thus we see that it is possible by our theory to determine the velocity
of the electron from the ratio of the magnetic power of deflexion
.
Thus we see that it is possible by our theory to determine the velocity
of the electron from the ratio of the magnetic power of deflexion 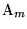 to the electric power of deflexion
to the electric power of deflexion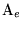 ,
for any velocity, by applying the law
,
for any velocity, by applying the law - From the deduction for the kinetic energy of the electron it follows that between the potential difference, P, traversed and the acquired velocity v of the electron there must be the relationship
- We calculate the radius of curvature of the path of the electron when a magnetic force N is present (as the only deflective force), acting perpendicularly to the velocity of the electron. From the second of the equations (A) we obtain
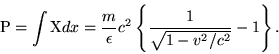
In conclusion I wish to say that in working at the problem here dealt with I have had the loyal assistance of my friend and colleague M. Besso, and that I am indebted to him for several valuable suggestions.
Footnotes
- 1.
- The preceding memoir by Lorentz was not at this time known to the author.
- 2.
- i.e. to the first approximation.
- 3.
- We shall not here discuss the inexactitude which lurks in the concept of simultaneity of two events at approximately the same place, which can only be removed by an abstraction.
- 4.
- ``Time'' here denotes ``time of the stationary system'' and also ``position of hands of the moving clock situated at the place under discussion.''
- 5.
-
The equations of the Lorentz transformation may be more simply deduced
directly from the condition that in virtue of those equations the relation
x2+y2+z2=c2t2
shall have as its consequence the second relation
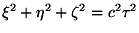 .
. - 6.
- That is, a body possessing spherical form when examined at rest.
- 7.
- Not a pendulum-clock, which is physically a system to which the Earth belongs. This case had to be excluded.
- 8.
-
If, for example, X=Y=Z=L=M=0, and N
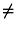 0, then from reasons of symmetry it is clear that when v changes
sign without changing its numerical value,
0, then from reasons of symmetry it is clear that when v changes
sign without changing its numerical value, 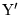 must also change sign without changing its numerical value.
must also change sign without changing its numerical value. - 9.
- The definition of force here given is not advantageous, as was first shown by M. Planck. It is more to the point to define force in such a way that the laws of momentum and energy assume the simplest form.
Editor's Note
- *
- Editor's note: In the original 1923 English edition, this phrase was erroneously translated as ``plain figures''. I have used the correct ``plane figures'' in this document.
About this EditionNumbered footnotes are as they appeared in the 1923 edition; an editor's note is marked by an asterisk (*) and appears in sans serif type. The 1923 English translation modified the notation used in Einstein's 1905 paper to conform to that in use by the 1920's; for example, c denotes the speed of light, as opposed the V used by Einstein in 1905. This electronic edition was prepared by John Walker in November 1999. You can download a ready-to-print PostScript file of this document or the LaTeX source code used to create it from this site; both are supplied as Zipped archives. This HTML document was initially converted from the LaTeX edition with the LaTeX2HTML utility and the text and images subsequently hand-edited to produce this text. Does the Inertia of a Body Depend upon its Energy-Content?Explore Relativistic Spaceflight in our C-shipDownload this document as LaTeX Source or PostScriptPhysics and General Relativity at FourmilabFourmilab Home Page |