Let two inertial co-ordinate systems (ICR's),
S and ![]() ,
be in standard configuration. This means that
,
be in standard configuration. This means that![]() is moving with constant velocity
is moving with constant velocity ![]() relative to S in the x-direction as in the following figure
relative to S in the x-direction as in the following figure
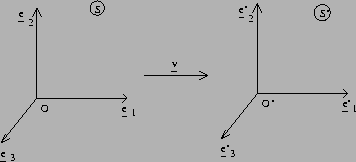
and that the spatial origins, O and ![]() ,
and the three spatial axes,
,
and the three spatial axes, ![]() and
and ![]() ,
co-incide at time
,
co-incide at time ![]() .
.
We shall convert units of time (eg. seconds) to a length (eg. meters)
by multiplying time by the speed of light c - thus our measure of
time will be ct which has units of length (this assumes implicitly
that c is the same in both reference frames - one of the postulates
of relativity). We wish to determine Cartesian co-ordinates in ![]() ,
, ![]() ,
as functions of Cartesian co-ordinates in S, (ct,x,y,z),
using reasonable assumptions. In other words
,
as functions of Cartesian co-ordinates in S, (ct,x,y,z),
using reasonable assumptions. In other words ![]() will be a function of ct,x,y and z, i.e.
will be a function of ct,x,y and z, i.e. ![]() ,
etc. It will sometimes be convenient to adopt an index notation where the
four co-ordinates (ct,x,y,z)
are labelled by an index a taking on four possible values 0,1,2,3
with x0=ct,
x1=x, x2=y and x3=z
so that (ct,x,y,z)=(xa).
Similarly for primed co-ordinates an index notation is sometimes useful,
,
etc. It will sometimes be convenient to adopt an index notation where the
four co-ordinates (ct,x,y,z)
are labelled by an index a taking on four possible values 0,1,2,3
with x0=ct,
x1=x, x2=y and x3=z
so that (ct,x,y,z)=(xa).
Similarly for primed co-ordinates an index notation is sometimes useful, ![]() ,
where the prime is placed on the index so that the index itself can be
used to distinguish between the two co-ordinates systems. The change from (ct,x,y,z)=(xa)
to
,
where the prime is placed on the index so that the index itself can be
used to distinguish between the two co-ordinates systems. The change from (ct,x,y,z)=(xa)
to ![]() is called a co-ordinate transformation.
is called a co-ordinate transformation.
The derivation of the explicit form of the co-ordinate transformation
proceeds in four steps:
Step 1): The transformations are linear
Consider a clock moving with constant velocity, showing a time ![]() .
The path of the clock in S can be described by four functions
.
The path of the clock in S can be described by four functions![]() .
Since the clock is moving with constant velocity in Sequal increments
of
.
Since the clock is moving with constant velocity in Sequal increments
of ![]() must correspond to equal increments of the co-ordinates (xa)
labeling the position of the clock in S. Thus
must correspond to equal increments of the co-ordinates (xa)
labeling the position of the clock in S. Thus ![]() is constant and
is constant and ![]() .
Since
.
Since ![]() is moving with constant velocity relative to S, the clock must aslo
be moving with constant velocity in
is moving with constant velocity relative to S, the clock must aslo
be moving with constant velocity in ![]() hence the same argument implies that
hence the same argument implies that ![]() is constant and
is constant and ![]() .
Now treating
.
Now treating ![]() as functions of xa the chain rule for differentiation
implies
as functions of xa the chain rule for differentiation
implies
| = | 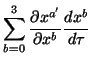 |
(1) | |
| = | 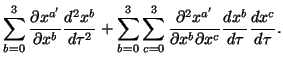 |
(2) |
Thus ![]() and
and ![]() can
only be true if
can
only be true if ![]() ,
in other words the transformations must be linear in xa.
In mathematical symbols this means
,
in other words the transformations must be linear in xa.
In mathematical symbols this means
| = | (3) |
where ![]() are constants and
are constants and ![]() are sixteen functions, independent of xa but possibly
depending on v - the velocity of S relative to
are sixteen functions, independent of xa but possibly
depending on v - the velocity of S relative to ![]() .
If S is in standard configuration relative to
.
If S is in standard configuration relative to ![]() then
then ![]() for all four values of a=0,1,2,3.
for all four values of a=0,1,2,3.
These conditions can be summarised in the single formula
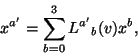
which can be thought of as a matrix formula with ![]() a
a ![]() matrix and
matrix and ![]() and
xa column vectors,
and
xa column vectors,
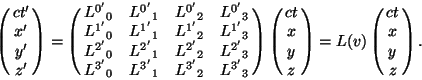
The matrix with components ![]() can be inverted to give
xa in terms of
can be inverted to give
xa in terms of ![]() ,
,

where L-1(v) is the inverse matrix to L(v),
i.e. ![]() with
with ![]() the identity matrix. Since the (xa) co-ordinate system
is moving in the negative
the identity matrix. Since the (xa) co-ordinate system
is moving in the negative![]() direction
relative to the
direction
relative to the ![]() with speed v it is clear that
with speed v it is clear that ![]() bear the same relation to (xa) as (xa)do
to
bear the same relation to (xa) as (xa)do
to ![]() ,
except that the sign of v is reversed. Mathematically this means
that L-1(v)=L(-v).
,
except that the sign of v is reversed. Mathematically this means
that L-1(v)=L(-v).
We shall now determine the sixteen functions ![]() .Step
2):
.Step
2): ![]()
At time ![]() the two planes
the two planes ![]() co-incide
for all y and z, as in the following figure
co-incide
for all y and z, as in the following figure

| (4) | |||
| (5) | |||
| (6) |
At time ![]() the two planes
the two planes ![]() co-incide. Since the relative motion is in the x-direction and there
is no rotation (by assumption), the planes
co-incide. Since the relative motion is in the x-direction and there
is no rotation (by assumption), the planes ![]() co-incide
co-incide ![]() as in the following figure
as in the following figure

thus
| (7) | |||
| (8) | |||
| (9) |
We can apply the same argument with S and ![]() interchanged,
which requires that we replace L(v) by L-1(v)=L(-v),
to deduce that
interchanged,
which requires that we replace L(v) by L-1(v)=L(-v),
to deduce that ![]() .
Hence
.
Hence ![]() .
.
Now if we reflect ![]() ,
without changing the other co-ordinates in S, it should be clear
that z and
,
without changing the other co-ordinates in S, it should be clear
that z and ![]() do
not change (since we have just proven that
do
not change (since we have just proven that ![]() is
independent of x). But changing the sign of xchanges the
sign of v, since the relative motion is in the
x-direction.
Hence
is
independent of x). But changing the sign of xchanges the
sign of v, since the relative motion is in the
x-direction.
Hence ![]() ,
thus
,
thus ![]() ,
so
,
so ![]() .
The sign can be determined by the trivial observation that v=0 should
give the identity transformation, thus
.
The sign can be determined by the trivial observation that v=0 should
give the identity transformation, thus ![]() .
.
A similar argument applied to the two planes ![]() allows
us to conclude that
allows
us to conclude that
and ![]() .
.
In summary, we have now that the transformation matrix must be of the form
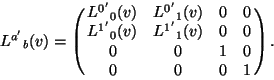
Up until now we have only really used the postulates of relativity
to streamline the notation. Now it will be used to full effect. First suppose
a flash of light is emitted from the origin O=(0,0,0) of S
at t=0 (and so also from the origin ![]() of
of ![]() at
at ![]() ).
The flash expands with the speed of light,
c which is the same
in both reference frames, as a spherical shell whose radius at time t
is given by x2+y2+z2=c2t2
in S and by
).
The flash expands with the speed of light,
c which is the same
in both reference frames, as a spherical shell whose radius at time t
is given by x2+y2+z2=c2t2
in S and by ![]() in
in ![]() .
Now we already know that
.
Now we already know that ![]() and
and ![]() so
so
Also
so
Demanding that this hold true for all t and any x
with |x|<ct gives three conditions
| 1 | (10) | ||
| 1 | (11) | ||
| 0 | (12) |
on four unkowns. We can express these as four functions of a single
parameter by using the identity ![]() for
any real
for
any real ![]() to write
to write
| (13) | |||
| (14) |
where ![]() is a function of v which is yet to be determined (the minus sign
is for later convenience). We have now arrived at the following form for
the transformation matrix:
is a function of v which is yet to be determined (the minus sign
is for later convenience). We have now arrived at the following form for
the transformation matrix:
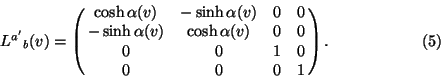
The spatial origin ![]() of
of ![]() is determined by
is determined by ![]() .
In S the point
.
In S the point ![]() moves with speed v in the x-direction, i.e. it has x
co-ordinate x=vt. Thus
moves with speed v in the x-direction, i.e. it has x
co-ordinate x=vt. Thus
so ![]() can be written as an inverse hyper-trigonometric function
can be written as an inverse hyper-trigonometric function
Note that the properties of the ![]() function now imply that -c<v<c (see the figure
below).
function now imply that -c<v<c (see the figure
below).![]() is called the rapidity of the transformation.
is called the rapidity of the transformation.
Using ![]() we have
we have
It is conventional to define
and then the transformation matrix can be written as
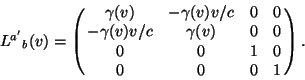
Thus we have finally arrived at the following form for the transformation
| = | (15) | ||
| = | (16) | ||
| = | y | (17) | |
| = | z. | (18) |
These are called Lorentz Transformations or sometimes Lorentz
Boosts, to distinguish them from rotations - the name ``boost'' is unfortunate
as there is no acceleration involved.
In matrix notation the Lorentz Transformations can be represented as
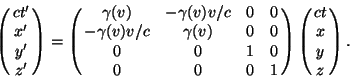
The rapidity has the useful property that it is additive
under successive transformations in the same direction with ![]() and
and ![]() .
This is most easily established using matrix multiplication to show that
.
This is most easily established using matrix multiplication to show that
(use the hyperbolic trigonometric identities
| = | (19) | ||
| = | (20) |
). Thus these two transformations are equivalent to a single transformation
with rapidity ![]() .
.