, c à d un ensemble U de sous-ensembles de que l'on nomme ensemble large qui satisfont :Mots clés : Hyperréelles, surréelles, infiniment petits, analyse non standard
A qui s'adresse ce texte ?
Premièrement à moi-même. Je me suis souvent intéressé à l'analyse non standard et à la définition des nombres infiniment petits, mais l'approche habituelle, axiomatique, me rebutait. Quand j'ai compris qu'on pouvait construire les nombres infiniment petits et infiniment grands, en se basant uniquement sur un seul "objet" bizarre, qui est un ultrafiltre non principal des entiers, j'ai été ravi. La construction ressemble beaucoup à la construction des nombres réels par les suites de Cauchy.
Je ne suis pas un spécialiste du domaine, même pas un amateur éclairé. Mais ne trouvant quasiment rien sur le web suivant l'approche que je décris ci-dessous, j'ai décidé de mettre ceci dans mes pages web.
Je ne sais pas si la description qui suit est exactement équivalente à celle faite par l'analyse non standard. Moi elle me plait, et m'éclaire sur la manière de voir et manipuler les nombres infinitésimaux.
"Construction" des nombres infiniment petits et infiniment grand.
La construction se base sur un ultrafiltre non principal des entiers , c à d un ensemble U de sous-ensembles de que l'on nomme ensemble large qui satisfont :
contenant un ensemble large est large., soit lui soit son complémentaire est large.Remarque :
Un ultrafiltre non principal des entiers n'est pas "constructible", il nécessite l'axiome du choix pour montrer son existence.
Partons du principe que nous avons un tel ensemble U de sous-ensembles des entiers.
Propriété que l'on utilisera souvent des ultrafiltres non principaux.
Si l'union de deux ensembles est large, et leur intersection est vide ou de cardinalité finie, alors un et un seul d'entre eux est large.
Démonstration :
Soient A et B deux ensembles larges.
Si A n'est pas large, alors sont complémentaire ~A l'est.
Comme B É (AÈ B)Ç (~A) qui est l'intersection de deux ensembles larges, B est large. CQFD1.
Si A et B étaient large, leur intersection serait large. Ce qui est impossible car un ensemble de cardinalité finie ne peut pas être large. CQFD
Conséquence :
Toute union finie d'ensembles non larges est non large.
Relation d'équivalence et ensembles non-standards
Pour tout ensemble A, on peut définir l'ensemble A
des suites à valeurs dans A.
Sur A on peut définir la relation d'équivalence :
Soient deux suites de A : {an}, {bn} Î
A
{an} ~
{bn} ssi {n Î
t.q. an = bn } est un ensemble large.
Donc deux suites sont équivalentes, si elles prennent la même valeur sur un ensemble large d'indices.
Il est facile de voir que c'est une relation d'équivalence. La transitivité vient du fait que l'intersection de deux ensemble large est encore large. C'est la propriété 2 des ultrafiltres.
Donc pour tout ensemble A, on peut définir l'ensemble que l'on note *A des classes d'équivalences des suites de A. En abrégé : *A = A|~
Définition : On dit que ce nouvel ensemble *A est l'ensemble non standard associé à A.
Notation : Notons *{an} les éléments de *A. *{an} est la classe d'équivalence de {an} Î
A.
Remarquons que toutes les relations et fonctions peuvent être vues comme des ensembles. Donc elles peuvent être étendues à leur équivalent non-standard.
Par exemple, une application f : A -> B correspond à l'ensemble : { (x, f(x) Î AxB t.q. x Î A }. Donc on peut lui associer son application non-standard : *f : *A -> *B correspondant à l'ensemble *{ (x, f(x) Î AxB t.q. x Î A }.
Pour mieux comprendre, soit *{an} Î *A. On peut lui associer *{f(an)} Î *B.
Si {an} ~
{bn} alors {f(an)} ~
{f(bn)},
donc cela défini la fonction *f : *A -> *B associée à f : A -> B
Remarquons aussi que : *A x *B = *(A x B).
Car si *{an} Î *A, *{bn} Î *B, on peut faire correspondre *{( an, bn)} Î *(A x B)
Réciproquement, si
an ~ a'n sur un ensemble large et
bn ~ b'n sur un ensemble large, alors
(an, bn) ~ (a'n, b'n) sur un ensemble large car l'intersection d'ensembles larges est large.
Donc à : *{( an, bn)} Î *(A x B) on peut faire correspondre *{an} Î *A, *{bn} Î *B.
Conclusion, pour un nombre fini d'ensembles, A1, A2, ... , Ak, on a :
*A1 x ... x *Ak = *(A1 ... x Ak)
Remarques :
On a l'inclusion naturelle de A dans *A en considérant les classes d'équivalences des suites constantes comme les éléments de A.
Notons i : A -> *A, l'inclusion.
Nous noterons par la même lettre " i " l'inclusion de B dans *B
On a la propriété : *f ° i = i ° f
Remarquons encore que si A est un ensemble de cardinalité finie, alors A = *A.
Car si pour *{an} Î
*A on note Ea = { n Î
t.q. an = a } pour a Î
A, il y a un nombre fini de tel ensemble, et exactement un et un seul sera un ensemble large. L'indice correspondant sera donc l'élément de A équivalent à la suite {an}.
Cas des nombres réels : 
Entrons dans la partie intéressante du sujet, c à d, la définition des nombres infinitésimaux.
Si représente l'ensemble des nombres réels, * est une extension des nombres réels. L'addition, la multiplication, la relation d'ordre, etc. sont des applications de x -> donc sont étendues comme applications de * x * -> *.
Montrons par exemple que tout élément non nuls de * possède un inverse.
Si {an} est un représentant d'un élément non nul de *, alors an ¹
0 sur un ensemble large.
Donc si (bn = 1/an quand an ¹ 0) et (bn = 1 quand an = 0), alors
*{bn} est l'inverse de *{an},
car bn ×
an =1 sur un ensemble large.
On obtient ainsi une extension de corps, i.e. * est un corps contenant .
Montrons aussi que * est totalement ordonné.
Soient *{an} et *{bn} Î
*, puisque soit un ensemble, soit son complémentaire est large, on a :
Soit an £
bn sur un ensemble large,
soit an ³
bn sur un ensemble large.
Ceci défini donc une relation d'ordre totale sur *.
Définition : Les nombres de * sont appelés les nombres hyperréels.
Définition : Les nombres de * qui ne sont pas réels, sont dit non-standards. Ceux qui sont réels, sont dit réels, ou standards.
Nombres standards
En utilisant la relation d'ordre totale, on va pouvoir définir une application
S : * -> È
{+¥
, -¥
}
On dit que S(*{an}) correspond à la partie standard de *{an} Î
*.
S(*{an}) = +¥ si pour tout nombre réel x, an > x sur un ensemble large.
S(*{an}) = -¥ si pour tout nombre réel x, an < x sur un ensemble large.
Sinon, S(*{an}) = la partie standard de *{an} que l'on va définir à partir de la suite emboîtée décrite ci-dessous :
Si on n'est pas dans un des deux premiers cas, il existe un nombre b Î
tel que
-b £ an £ b sur un ensemble large.
On peut procéder de manière dichotomique :
Soit -b £ an £ 0 sur un ensemble large.
Soit 0 £ an £ b sur un ensemble large.
car soit un ensemble, soit son complémentaire est large.
On peut répéter en subdivisant l'intervalle correspondant à l'ensemble large, pour obtenir une suite d'intervalles emboîtés. L'intersection de ces intervalles définit un nombre réel qui est par définition la partie standard de *{an}.
Définition : *{an} - S(*{an}) est la partie non standard de *{an}.
Elle est plus infinie si S(*{an}) = +¥
Elle est moins infinie si S(*{an}) = -¥
Définition : On dit que le nombre hyperréel *{an} est fini, si S(*{an}) Î
. Sinon on dit qu'il est infiniment grand, positivement ou négativement.
Propriétés de l'application S : * -> È
{+¥
, -¥
}
i S
---> * ---> È
{+¥
, -¥
}
La composition de S avec i donne l'identité sur les réels.
L'application S préserve les opérations d'additions, de soustractions, de multiplications, de divisions et de relation d'ordre avec égalité, pour les nombre hyperréels finis.
Mathématiquement, cela s'écrit :
Soient *{an} et *{bn} Î
* deux nombres hyperréels finis. On a :
S(*{an} + *{bn}) = S(*{an}) + S(*{bn})
S(*{an} - *{bn}) = S(*{an}) - S(*{bn})
S(*{an} × *{bn}) = S(*{an}) × S(*{bn})
S(*{an} / *{bn}) = S(*{an}) / S(*{bn}) si S(*{bn}) ¹ 0
*{an} < *{bn} <=> S(*{an}) £ S(*{bn})
Voici enfin la définition des nombres infiniment petits
Si S(*{an}) = +¥ on dit que *{an} est un nombre infiniment grand positivement.
Si S(*{an}) = -¥ on dit que *{an} est un nombre infiniment grand négativement.
Si S(*{an}) = 0 on dit que *{an} est un nombre infiniment petit.
Remarque : Le seul nombre réel infiniment petit est 0.
De prendre 0 dans les infiniment petits est une convention que j'ai toujours vue en analyse non standard.
Parler de nombres hyperréels positif et négatifs est bien défini, car l'ordre sur * est total.
Applications définies sur un sous ensemble des nombres réels.
Soit A Ì
et f : A -> . Alors *f : *A -> * est aussi bien défini.
Par exemple, si A = [0, +¥ ) = l'ensemble des nombres réels non négatifs, alors *A contient les nombres hyperréels positifs. En particuliers, *A contient les infiniment petits positifs, mais pas les infiniment petits négatifs.
Conclusion :
On a défini rigoureusement une extension des nombres réels, qui contient des nombres que l'on peut assimiler à des nombres infiniment petits et des nombres infiniment grands. Autour de chaque nombre réel, gravite un ensemble de nombres hyperréels infiniment proche du nombre donné.
Définition : On dit que deux nombres de * sont infiniment proche, si la partie standard de leur différence est nulle.
Remarquons que deux nombres infiniment grands peuvent être infiniment proche.
Que deviennent les nombres entiers et rationnels ?
On peut bien sûr définir *, *
, *
, etc. Donc on a des entiers non standards, des rationnels non standards etc.
L'application "partie standard" S : * -> est à valeurs dans et pas dans !
Attention aussi que Ë
*
Donc autour de chaque nombre réel, il y a un "nuage" de nombres rationnels non standards, infiniment proche du nombre réel donné.
Remarque :
Intuitivement, on ne comprend pas ce qui signifierait des entiers non standards fini. Heureusement, cela n'existe pas, comme nous allons le montrer :
Soit {an} une suite de nombres entiers.
Notons Ek = { n Î
t.q. an = k } et Fk = { n Î
t.q. an > k }
Si *{an} représente un entier fini, alors il existe un entier " k0 " tel que Fk0 n'est pas un ensemble large. Donc un des ensemble Ek pour k < k0 est un ensemble large, car ils sont en nombre fini, disjoints et leur union égale le complémentaire de Fk0. Donc la suite {an} est équivalente à la suite constante correspondant à l'indice de l'ensemble Ek qui est large. Cela signifie que *{an} est un entier standard.
Le même argument peut être fait pour l'ensemble des entiers relatifs.
Remarque :
Est-ce que tout nombre entier infini peut être représenté par une suite croissante?
Je ne connais pas la réponse à cette question.
J'ai essayé avec la suite suivante : On peut penser qu'il existe une suite {an} qui soit telle que pour tout nombre "a" entier, an = a sur un ensemble infini non large. Cette suite représente un entier infini. Mais il est possible qu'elle n'admette un représentant formé par une suite croissante.
Justifions que cette suite {an} représente un nombre infini. Puisque {an} = 1 sur un ensemble non large, an = 2 sur un ensemble non large, etc. Donc pour tout entier "a", an < a sur une union finie d'ensemble non large, qui est donc non large comme on l'a vu dans l'introduction. Donc {an} ne représente pas un nombre fini.
Applications : Nouvelle définition de la limite.
Avant de continuer, il faut faire attention en remarquant que le choix initial d'un ultrafiltre non principal sur les entiers n'est pas unique. Donc si une propriété dépend de l'ultrafiltre, on ne pourra pas en faire grand chose, en particulier la partie standard dépendra aussi de l'ultrafiltre. Par exemple la suite {an} = {(-1)n} est équivalente à -1 ou à +1 suivant l'ultrafiltre choisi. Par contre on sait que dans tous les cas elle vaut soit -1 soit +1.
Soit f : -> une fonction. Soit a Î
.
Définitions :
On dit que L Î
est limite de f(x) pour x tendant vers "a" si
*{an} infiniment proche de "a" implique *{f(an)} est infiniment proche de "L".
Montrons que cette définition est la même que la définition habituelle de limite.
Premièrement, supposons que "L" soit la limite au sens habituelle.
Soit *{an} infiniment proche de "a"
A voir que *{f(an)} est infiniment proche de "L", i.e.
à voir que pour tout e
> 0, |f(an) - L| < e
sur un ensemble large.
Soit un e > 0 donné.
Par hypothèse, il existe d > 0 t.q. si |an - a| < d , alors |f(an) - L| < e .
Pour ce nombre d , on sait que |an - a| < d sur un ensemble large, donc sur ce même ensemble large on a : |f(an) - L| < e CQFD
Montrons la réciproque :
Montrons que si "L" n'est pas limite au sens classique, alors "L" n'est pas non plus limite avec la nouvelle définition.
Si il existe e
> 0 t.q. quelque soit n Î
il existe an Î
t.q. |an - a| < 1/n et |f(an) - L| > e
, alors
*{an} est infiniment proche de "a", mais *{f(an)} n'est pas infiniment proche de "L". CQFD
On a donc une nouvelle manière de définir des limites, équivalente à l'ancienne manière. La définition de continuité de fonction en un point en découle.
Définition :
Une fonction f : -> est continue en un point d'abscisse "a" si "f" est définie en "a" et si l'image par "f" de n'importe quelle nombre infiniment proche de "a" est infiniment proche de f(a).
Mathématiquement cela s'écrit : S(*x - a) = 0 => S(*f(*x) - f(a)) = 0, où *x Î
*.
Définition :
Pour la dérivée de la fonction en un point d'abscisse "a" :
Si la partie standard de 
est indépendante de *x Î
*, *x ¹
a et *x infiniment proche de "a", alors la fonction est dérivable en "a" et la valeur de la partie standard est la dérivée de la fonction "f" en "a".
Cette définition est compatible avec la définition classique de dérivée.
Montrons que dérivable implique continue.
Supposons que "f" soit dérivable en "a".
Rappelons que S(*x) = la partie standard de *x.
Si *x est infiniment proche de "a", i.e. S(*x-a) = 0.
A voir que *f(*x) est infiniment proche de f(a), i.e. que S(*f(*x) - f(a)) = 0.
Soit *x infiniment proche de "a".
S(*f(*x) - f(a)) = S
= S×
S(*x-a) = nombre ×
0 = 0
Définition :
Une fonction f : -> est uniformément continue sur A si
Pour tout *x, *y Î *A, si *x-*y est infiniment petit, alors *f(*x)-*f(*y) est infiniment petit.
Montrons que cela est équivalent à la définition classique.
Si la définition classique est fausse, alors :
Il existe e > 0, t.q. pour tout "n" entier, il existe xn, yn t.q. |xn-yn| < 1/n et |f(xn)-f(yn)| > e
Cela défini deux suites {xn} et {yn} représentant des nombres infiniment proches, t.q.
*{f(xn)} et *{f(yn)} ne soit pas infiniment proche. CQFD
Réciproquement :
Soient *{xn} et *{yn} représentant des nombres infiniment proches.
Donc pour tout d > 0, |xn-yn| < d sur un ensemble large.
Soit e > 0 donné.
Par hypothèse, il existe d > 0 t.q. |xn-yn| < d implique |f(xn)-f(yn)| < e
Donc, puisque |xn-yn| < d sur un ensemble large, on a aussi |f(xn)-f(yn)| < e sur un ensemble large. CQFD.
Exemple :
Soit f : (0, 1] -> , f(x) = 1/x.
Montrons que cette fonction n'est pas uniformément continue.
Remarquons que *(0, 1] contient tous les hyperréels infiniment petits positifs.
Donc *{an = 1/n} et *{bn = 1/n2} représentent deux hyperréels de *(0, 1] infiniment proches, mais leur image par *f qui sont *{f(an)=n} et *{f(bn)=n2} ne sont pas infiniment proche.
Le théorème suivant est un classique, qui devient tout simple.
Théorème :
Si A = [a,b] est un intervalle fermé et borné, alors
Toutes fonction continue sur [a, b] est aussi uniformément continue sur [a, b].
Démonstration :
Remarquons que :
1 ) Puisque A est borné, la partie standard de tout hyperréel de *A est finie.
2) Puisque A est fermé, la partie standard de tout hyperréel de *A est dans A.
Soient *x, *y deux hyperréels de *A infiniment proches.
Soit "a" leur partie standard, qui est finie et dans A selon les deux remarques.
S(*f(*x)-*f(*y)) = S(*f(*x)-f(a)) + S(f(a)-*f(*y)) = 0 + 0 = 0. CQFD (facile !)
Montrons la continuité de quelques fonctions :
Dans les lignes qui vont suivre, *h représentera un hyperréel infiniment petit, non nul.
montrons que l'application racine carrée est continue.
Soit "a" un nombre positif ou nul.
(S(racine(a + *h)))2 = S(a+*h) = a, donc
S(racine(a + *h)) = racine(a), ce qui montre la continuité de la fonction racine.
Plus généralement, la fonction x -> xp/q est continue sur [0, ¥ ) car
(S((a + *h)p/q))q = S((a+*h)p) = S(ap+*h× (nombre)) = ap, donc
S((a + *h)p/q) = a p/q, ce qui montre la continuité.
La continuité de la somme, produit etc. de fonction se déduit directement des propriétés de la fonction "partie standard".
S(*(f× g)(*x)) = S(*f(*x))× S(*g(*x)) = f(x)× g(x) = (f× g)(x), ce qui montre la continuité du produit.
Montrons que sin(*h) est infiniment petit, si *h l'est aussi.
Si -1 < x < y < 1, alors sin(x) < sin(y). Donc cela est aussi vrai pour des hyperréels.
Si *h est infiniment petit, alors
pour tout y > 0 réel -y < *h < y. Donc -sin(y) < sin(*h) < sin(y).
On a montré que sin(*h) est plus petit que tout réel positif et plus grand que tout réel négatif, donc c'est un infiniment petit.
De même on montre que cos(*h) -1 est infiniment petit si *h l'est aussi.
On peut par exemple utiliser le fait que cos2(x) + sin2(x) = 1 pour la démonstration.
Montrons que S(sin(*h)/(*h)) = 1, si *h est infiniment petit.
|sin(*h)| < |*h| et |tan(*h)| > |*h|. Donc
cos(*h) < sin(*h)/*h < 1
En prenant la partie standard des deux cotés, on termine la démonstration.
On montre aussi que (cos(*h)-1) / *h est infiniment petit si *h l'est.
Dérivée de la fonction sinus.
(sin(a+*h) - sin(a)) / *h = sin(a)× (cos(*h)-1) / *h + cos(a)× sin(*h) / *h
En prenant la partie standard, on obtient la dérivée de la fonction sinus en "a".
Asymptotes.
On peut donner ici une définition plus générale que habituellement, sans complications supplémentaires.
Définition :
On dit qu'une fonction g : -> est une asymptote d'une fonction f : -> si la fonction *(f - g) prend des valeurs infiniment petites sur des hyperréels infiniment grands.
Le cas particulier où g(x) = a× x + b est une application affine est très important.
Exemple, cas où f(x) = racine(a× x2 + b× x + c) :
racine(a× x2 + b× x + c) = x× racine(a + b / x + c / x2) = x× racine(a) + b / (2 × racine(a)) + (...) / x
Le troisième terme est infiniment petit quand "x" est infiniment grand, donc on a trouvé une droite affine, qui est une asymptote de f(x) = racine(a× x2 + b× x + c).
Dans le fond du problème, on utilise les même techniques que avec les limites classiques, mais il y a moins de détails autour.
Les démonstrations de dérivation de produit de fonctions, quotients, composition et réciproque ne se font pas plus simplement ici. Une méthode classique trouvée par Carathéodory en 1950 est bien meilleur que les démonstrations classiques.
Voici une parenthèse, pour montrer classiquement les formules de dérivations de fonctions.
Formulation de Carathéodory, (1950 p.121).
J'ai suivit le l'excellent livre de E. Hairer et G.Wanner, "L'analyse au fil de l'histoire" ed. springer.
La fonction f : -> est dérivable au point d'abscisse "a", si et seulement si il existe une fonction j
: -> continue en au point d'abscisse "a", telle que
f(x) = f(a) + j (x) × (x-a).
La valeur j (a) est la dérivée f'(a) de la fonction "f" en "a".
Pour x ¹ a, on a j (x) = (f(x) - f(a)) / (x - a)
Montrons que (f× g)' = f'× g + f× g'
Par hypothèse,
f(x) = f(a) + j (x) × (x-a) et g(x) = g(a) + y (x) × (x-a). Donc
(f× g)(x) = (f(a) + j (x) × (x-a)) × (g(a) + y (x) × (x-a))
= f(a)× g(a) + (f(a)× y (x)) + j (x)× g(a) + j (x)× y (x)× (x-a)) × (x-a)
Le facteur qui multiplie (x-a) est continue et en x=a, il vaut f(a)× g'(a) + f' (a)× g(a). CQFD
Montrons que (g°f)'(a) = g'(f(a)× f'(a)
Par hypothèse,
f(x) = f(a) + j (x) × (x-a) et g(y) = g(f(a)) + y (y) × (y - f(a)), avec y (f(a)) = g'(f(a)).
En remplaçant "y" par f(x), on a:
(g°f)(x) = g(f(x)) = g(f(a)) + y (f(x)) × (f(x) - f(a)) = g(f(a)) + y (f(x)) × j (x) × (x-a)
Denouveau, le facteur qui multiplie (x-a) est continue,
et en x=a, il vaut g'(f(a)) × f'(a) CQFD
Montrons que rf'(y) = 1 / f'(f(y) ou rf est la fonction réciproque de f.
Par hypothèse,
f(x) = f(a) + j (x) × (x-a) et j (a) = f'(a) ¹ 0.
Si y = f(x) et b = f(a), alors x = rf(y) et a = rf(b). Donc
y = b + j ( rf(y)) × (rf(y) - rf(b)) donc
r
f(y) = rf(b) + (y - b) / j ( rf(y)).Le facteur qui multiplie (y - b) est continue et vaut 1 / f'(f(a)) en y = b. CQFD
Fin de la parenthèse sur la formulation de Carathéodory pour montrer les formules de dérivation.
Passons aux infiniment grands.
Avec les infiniment petits, l'intuition nous guide bien. Par contre, j'avais toujours de la peine à me représenter les infiniment grands, et les sommes infiniment grandes. Maintenant, avec les définitions précises des nombres hyperréels, on peut faire des sommes dont l'indice supérieur est infiniment grand. Voyons cela de plus près :
Soit {pn} une suite de nombre réels, tout à fait classique. On peut définir l'application :
Sum : -> ,
Sum(k) = p1 + .. + pk
Donc l'application Sum s'étend en une application *Sum : * -> *.
Si *n est un entier infiniment grand, que représente *Sum(*n) ?
C'est comme une somme infinie de termes.
Par exemple, si les pk sont tels que Sum(k) = k× (-1)k que représente *Sum(*n) ?
Prenons le cas où *n représente la suite des entiers = {1, 2, 3, ...}
*Sum(*n) est représenté par la suite {-1, 2, -3, 4, -5, 6, ... } qui représente un nombre hyperréel. Mais est-il positif où négatif ? Cela dépend de l'ultrafiltre choisi pour la construction des hyperréels, donc la réponse n'est pas très intéressante. La seul chose indépendante de l'ultrafiltre est que la partie standard de ce nombre n'est pas finie.
Autre exemple.
Si Sum(k) = (-1)k alors *Sum(*n) est représenté par la suite {-1, 1, -1, 1, -1, 1, ... } qui représente un nombre hyperréel. De Nouveau, le signe de ce nombre dépend du choix de l'ultrafiltre. Mais on constate aussi que si *n est représenté par la suite {2, 4, 6, 8, ...}, alors *Sum(*n) = 1, qui est un nombre réel. Par contre pour *n représenté par la suite {3, 5, 7, ...}, *Sum(*n) = -1, qui est un autre nombre réel.
Proposition :
Si pour tout nombre entier infini *n Î
*, la partie standard de *Sum(*n) est le même nombre réel "L", alors la suite Sum(k) converge classiquement vers ce même nombre réel "L". La réciproque est aussi vraie. Ceci donne une nouvelle définition de la convergence d'une suite, qui est compatible avec l'ancienne.
Je ne sais pas à quoi cela sert, mais c'est joli de comprendre la signification d'une somme infinie de nombre. C'est joli de voir que toute somme infinie de nombres a toujours une signification, même si celle-ci dépend d'un choix initial d'ultrafiltre et qu'il n'y a de choix privilégié.
Démonstration :
Supposons que Sum(n) ne converge pas vers le nombre réel "L".
Donc, il existe e
> 0 tel que pour tout n Î
, il existe un entier an > n tel que |Sum(an) - L| > e
Cela défini une suite {an} représentant un entier infini tel que *Sum(*{an}) ne soit pas infiniment proche de "L", puisque |Sum(an) - L| > e
sur qui est un ensemble large. Ceci contredit l'hypothèse. CQFD.
Montrons la réciproque
Supposons que Sum(n) converge vers "L" pour "n" tendant vers l'infini.
Soit {an} représentant d'un entier infini.
A voir que *Sum(*{an}) est infiniment proche de "L", i.e.
que pour tout e > 0, |Sum(an) - L| > e sur un ensemble large.
Soit e > 0 donné. Par hypothèse, il existe un entier "N" tel que n > N => |Sum(n) - L| > e .
Comme an > N sur un ensemble large, on a bien |Sum(n) - L| > e sur un ensemble large. CQFD
La grosse partie qui devrait venir, correspond au chapitre sur l'intégration.
Juste pour le fun, voici une définition de l'intégral au sens de Riemann généralisé, connue aussi sous le nom de "gauge integral" ou intégral de Kurzweil (1957). Elle est plus simple que la définition de l'intégral de Lebesgue (1902) et plus générale. Tous les théorèmes classique s'y retrouvent, avec moins d'hypothèses en général.
Définition :
On dit qu'une fonction f : -> est intégrable sur l'intervalle (a,b) au sens de Riemann généralisé, et vaut L, si
"
e
> 0, $
d
: -> + tel que pour tout partition d
- fine,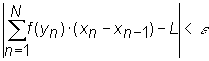 
Rem. d est une fonction quelconque, à valeurs strictement positifs.
Rem. Un partition d
- fine est la données de deux suites finies de nombres
{xn} et {yn}, n=0..N, satisfaisant :
a = x0 £ y1 £ x1 £ y2 £ x2 £ ... £ xN-1 £ yN £ xN = b et xn - xn-1 < d (yn), n=1..N
La nouveauté est la fonction d au lien du nombre d > 0.
Avec cette définition, toutes les fonctions intégrables au sens de Lebesgue sont intégrables. Les fonctions intégrables au sens de Lebesgue sont exactement toutes les fonctions absolument intégrables.
Comment utiliser les nombres hyperréels pour définir autrement l'intégrale ?
Ce document se trouve sur mes pages web sur :
http://www.juggling.ch/gisin/math/hyperreals/hyperreels_main.html
e d Í Î Ï Ì Ê É Ë » º ~ ¹ £ ³ +¥ × " $
*,
*,
*,
*
math.html
hyperreels_main.html
hyperreels.html
( = http://www.juggling.ch/gisin/math/hyperreals/hyperreels.html )